Ondas que nos Rodean: OSCILACIONES II: Movimiento Amortiguado y Forzado

Movimiento oscilatorio amortiguado

Cualquier sistema oscilante libera energía hacia el medio que le rodea. Como en cada periodo gasta cierta fraccion de la energia inicial con la cual comenzo a moverse, en consecuencia, su amplitud y velocidad tambien decrecen en el tiempo; después de varias oscilaciones, dependiendo de la intensidad con la cual interactúa con el medio que le rodea, el sistema se detiene. Toda la energía que tenía pasó como energía térmica al ambiente, por efecto de las fuerzas de fricción que intervienen en el proceso.

A continuación se analiza el movimiento oscilatorio amortiguado de un cuerpo de masa M sometido a la acción de una fuerza disipativa con dependencia proporcional de la velocidad (f v = - λ v ), donde λ es el coeficiente de fricción o viscosidad; además de la fuerza restauradora (f k = -kx). Al realizar un análisis detallado de un sistema simple con estas características, se obtiene que la ecuación diferencial que describe su movimiento es:

d ² x /dt ² + λ dx /dt + ω o ² x = 0, donde la frecuencia angular natural es ω o = 2 πf o = (k/M) ^1/2, yf o es la frecuencia natural de vibración.

La solución de esta fórmula diferencial es:

x(t) = x _o e ^-t/^τ sen ( ω t + φ ),

donde x _oes la amplitud de las oscilaciones, τ el tiempo de relajación del sistema, es decir el intervalo de tiempo que debe transcurrir para que su amplitud x _o disminuya hasta x _o/e (e = 2,7182), la frecuencia angular sin amortiguamiento viene dada por: ω = [ ω _o² - (λ/2M) ] ^1/2y φ es el ángulo de fase.

Por consiguiente, esta frecuencia natural amortiguada ω es menor que la frecuencia natural ω_o, debido al efecto disipador de energía.

Por supuesto, la velocidad será:

v(t) = dx/dt = x _o e ^-t/τ [-(1/τ) sen (ω t + φ) + ω cos(ω t + φ)].

Como en esta última expresión aparece el factor e ^-t/τ, se concluye que la velocidad decae también exponencialmente con el tiempo.

A continuación, es interesante analizar el efecto que tiene la disipación de la energía a través de la fricción, sobre el movimiento del sistema; dependiendo del valor del coeficiente de viscosidad λ en comparación con los parámetros que caracterizan al sistema, este oscila o no; oscila o amortigua. A partir de la relación de ω se puede comparar λ con 2(λM) ^1/2^, o el periodo To con el tiempo de distension del sistema, el cual es 2πτ. En tal sentido se pueden diferenciar cuatro casos de particular interés, a saber:

a) MAS cuando λ = 0 ,

b) sub amortiguado cuando ω > 0, lo que es equivalente a

λ < 2(kM) ^1/2, o T o < 2πτ ,

c) críticamente amortiguado sí

λ = 2(kM) ^1/2, o T o = 2πτ , y

d) sobre amortiguado si

λ > 2(kM) ^1/2, o T o > 2πτ.

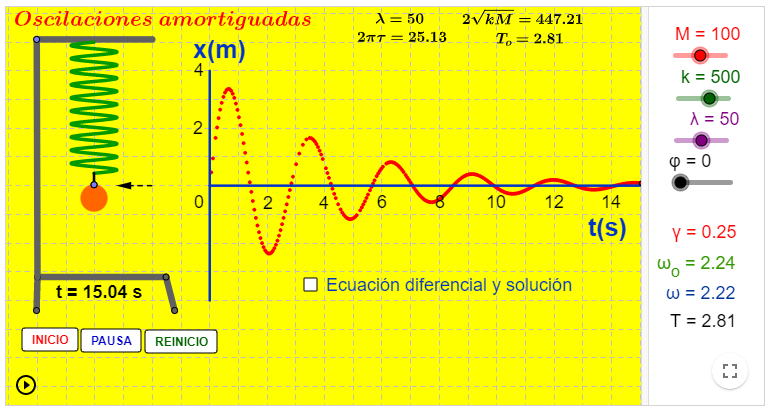
A continuación se muestran dos applets que permiten simular y analizar el comportamiento de este tipo de sistema mecánico. El de la figura 1.9 simula el movimiento de un sistema masa resorte amortiguado, aunque no se muestra el mecanismo disipador de energía. Se puede variar M (masa), k (constante elástica), λ (constante de amortiguamiento) y φ (ángulo de fase) con los respectivos deslizadores. Se puede observar cómo disminuye la amplitud x _oa medida que el sistema oscila. Con el mismo se puede hacer la correspondiente gráfica del desplazamiento x(t) . Abajo se muestra la fórmula diferencial con su respectiva solución para x(t) . Debajo de los deslizadores se pueden leer los valores de la frecuencia natural ω o , la frecuencia natural amortiguada ω y el periodo T.

Disponible en: https://www.geogebra.org/m/sqAAUqqy

Actividades:

Pulse el botón REINICIO y luego el botón INICIO . Para los valores indicados ( M = 100 kg, k = 500 N/m y λ = 50 Kg/s ), el sistema oscila con movimiento amortiguado, y su desplazamiento en el tiempo lo da la gráfica adjunto. Observe que el período T es de 2.81 s, expresó como T = 2.81 en la parte inferior derecha del recuadro de deslizadores, y que también se puede leer directamente de la gráfica. También se calcula ω o y ω .

A continuación se analizan cuatro casos de singular interés:

1. El MAS . Si se elimina la viscosidad ( λ = 0 , ω = ω o ) se obtiene el MAS. Elija λ = 0 y pulse los botones de REINICIO e INICIO para activar el applet. Observe cómo las amplitudes se mantienen constantes porque el sistema no disipa energía.

Registro gráfico del MAS.

2. Movimiento sub amortiguado . El sistema oscila con movimiento amortiguado si λ < 2(kM)^1/2, o To <2πτ. Mientras mayor sea λ, más rápido se amortigua el movimiento. Varíe los valores de los parámetros para apreciar sus efectos. Al elegir, por ejemplo:λ = 60, M = 100 yk = 500, se obtiene que 2(kM)^1/2= 447, de modo tal que se cumplan las condiciones anteriores, como se muestra en la figura de abajo.

Registro gráfico del movimiento sub amortiguado.

3. Movimiento críticamente amortiguado. En este caso se cumple que λ = 2(kM)^1/2, o To =2πτ , y por consiguiente a partir de estos valores el sistema deja de oscilar. Elijaφ = π/2 de modo que la esfera inició su movimiento (t = 0) en el punto de retorno superior +xo . Varíe los valores de k, M y λ hasta que se cumplan las igualdades anteriores ; y el sistema inicia su movimiento desde +x o , hasta detenerse asintóticamente en el punto de equilibrio x = 0 , y puede desplegarse la gráfica exponencial x(t) del desplazamiento como se muestra en la figura adjunta correspondiente .

Registro gráfico del movimiento sobre amortiguado.

4. Movimiento sobre amortiguado. Cuando λ > 2(kM) ^1/2, o T o > 2πτ el sistema no oscila. Varíe los valores de k, M y λ hasta lograr las desigualdades anteriores. En este caso NO aparece el sistema masa recurso en el applet.

Por otra parte, con la finalidad de completar el análisis de este tipo de sistema mecánico, se dispone del siguiente applet, el cual simula el movimiento oscilatorio amortiguado de una esfera, aunque no se muestra el resorte elástico ni el mecanismo disipador de energía. El mismo permite graficar simultaneamente con las casillas x(t) y v(t), la posición y la velocidad del sistema; se pueden variar los diferentes parámetros con los deslizadores x _o (amplitud), M (masa), k (constante elástica), λ (coeficiente de amortiguamiento) y φ (ángulo de fase). La casilla Tau permite calcular τ , es decir, el intervalo de tiempo para que la amplitud x _o disminuya hasta 0,37 x _o ; también se muestra cómo determinar su valor directamente de la gráfica. Por otra parte, se calculan los valores de τ , ω y T. También contiene información teórica del sistema en la casilla Casos donde se describen los diferentes casos particulares a saber: MAS, sub amortiguado, críticamente amortiguado y sobre amortiguado; los cuales se pueden identificar comparando entre si los valores de λ con 2(kM) ^1/2, o T o con 2πτ , como se ha mencionado antes.

Disponible en: https://www.geogebra.org/m/mxnzwgwf

Actividades

1. Repetir lo indicado para el applet anterior.

Movimiento oscilatorio forzado.

resonancia

El sistema que se analiza a continuación tiene dos propiedades intrínsecas: la elasticidad y la inercia. Como se apareció antes, la elasticidad genera la fuerza elástica restauradora que actúa sobre el cuerpo cuando ha sido desplazada de su posición de equilibrio estable; la inercia da información acerca de cómo responde la masa M a la acción de la fuerza restauradora. Estas dos propiedades actúan simultáneamente sobre el sistema determina su movimiento, y en consecuencia este vibra u oscila con la frecuencia angular ω o = (k/M) ^1/2 . Por otra parte, cuando el sistema disipa energía, por medio de cualquier acción externa, su frecuencia se reduce a ω = [ ω _o² - (λ/2M) ] ^1/2; por consiguiente, vibra con más lentitud porque existe algo (la viscosidad en un sistema mecánico, por ejemplo) que se opone a su movimiento. Si además de la fuerza externa disipativa, el sistema se somete a la acción de una fuerza externa oscilante, que compense la pérdida periódica de energía, oscilará al principio con su frecuencia natural amortiguada hasta que se estabiliza, y finalmente seguirá oscilando con la frecuencia impulsora, en un caso; en otros casos, el sistema oscilará con la frecuencia impulsora desde el principio, pero cambiando la amplitud de las oscilaciones en el tiempo. Los diferentes casos se discutirán con los respectivos applets. Ver Tema Avanzado para la descripción teórica.

El applet de abajo simula un sistema masa resorte con estas características. Contiene los deslizadores M (masa), k (constante elástica), Fo (amplitud de la fuerza impulsora), ωf (frecuencia angular de la fuerza impulsora) y λ (coeficiente de viscosidad), que permiten controlarlo. Abajo se calculan ωf y ω, para poder comparar sus valores, y determinar así el tipo de movimiento que está ocurriendo. También se modela el caso asintótico correspondiente a movimiento forzado sin amortiguamiento (λ = 0), discutido ante, en dos situaciones diferentes: la resonancia y las pulsaciones. Con las casillas ubicadas en la parte inferior se pueden activar estos casos, según las ecuaciones xmax y x(t) (ver Tema Avanzado). Importante: este applet construye la gráfica punto por punto; dependiendo del explorador (Chrome, Firefox, entre otros) y del computador utilizado, puede que tarde algunos minutos en cargarlo para luego calcular. Si los puntos están muy dispersos, recomendamos activar varias veces el boton de Inicio.

Disponible en: https://tube.geogebra.org/m/2350467

Actividades:

Pulse el botón REINICIO y luego el botón INICIO. Para los valores indicados (M = 9 kg, k = 230 N/m, Fo = 200 N, ωf = 3 s^-1, λ = 4 kg/s), el sistema oscila en el estado transitorio y luego se estabiliza en el estado estacionario vibrando con la frecuencia ωf = 3 s^-1, como se indica en la figura 1.13.

A continuación se analizan cuatro casos de interés particular:

1. La frecuencia impulsora es mayor que la frecuencia del sistema (ωf >> ω). Para ωf = 5 s^-1, ω = 1 s^-1, Fo = 4.000 N, λ = 50 kg/s, se puede observar que el sistema comienza a oscilar en su estado transitorio con la frecuencia impulsora, pero modulada por la frecuencia natural, y rápidamente se estabiliza en su estado estacionario donde se impone la acción de la fuerza oscilante externa, como se observa en la gráfica de la figura siguiente. Se puede apreciar directamente de la gráfica que el sistema vibra con un período de 1,25 s.

Registro gráfico del desplazamiento para ωf >> ω .

2. La frecuencia impulsora es menor que la frecuencia del sistema (ωf << ω). Para ωf = 0,5 s^-1, ω = 3 s^-1, Fo = 1.000 N, λ = 100 kg/s, se puede concluir que el sistema comienza a oscilar en su estado transitorio con la frecuencia natural amortiguada, y rápidamente se estabiliza en su estado estacionario donde se impone la acción de la fuerza oscilante externa de nuevo, y pone vibrar al sistema con un período de 12,6 s.

Registro gráfico del desplazamiento para ωf << ω .

3. Resonancia. La frecuencia impulsora es igual a la frecuencia del sistema (ωf = ωo). En este caso, el sistema vibra con su frecuencia natural ωo modificada por la acción de la viscosidad; es decir vibra con la frecuencia ω. La fuerza externa impulsa al sistema con el mismo vaivén de la oscilación natural amortiguada; mejor dicho, el sistema oscila en sincronía con la fuerza impulsora. Bajo esta condición, aunque la amplitud de la fuerza impulsora sea pequeña, el sistema empieza a oscilar en un estado transitorio, y en cada oscilación incrementa la amplitud de sus oscilaciones, hasta alcanzar el estado estacionario donde la amplitud alcanza un máximo valor. Se dice entonces que el sistema entra en resonancia con la fuerza impulsora.

En primer lugar se analiza el modelo más sencillo del sistema sin amortiguamiento (λ = 0), para los siguiente valores: λ = 0, ωf = 3 s^-1, ω = 3 s^-1, Fo = 16 N, λ = 100 kg/s. El registro gráfico de la figura de abajo muestra este comportamiento; se observa que la amplitud se incrementa proporcionalmente al tiempo tal como expresa la ecuación 1.23.c: xmax = 0,5 ao/ωo t sen(ωf t) (ver Tema avanzado). Esta situación es de esperar, ya que no existe ningún proceso disipador de energía; así que la energía que cede el agente impulsor externo en cada oscilación, la utiliza el sistema en incrementar su amplitud. La curva verde continua se graficó con la ecuación 1.23.c y la curva azul a puntos es la gráfica de la solución general; por supuesto, coinciden.

Registro gráfico del desplazamiento para ωf = ω .

En segundo lugar, cuando se considera el amortiguamiento (λ > 0) con los siguientes valores: λ = 3 kg/s , ωf = 3 s^-1, ω = 3 s^-1, Fo = 6 N; la amplitud de las oscilaciones crece en la etapa transitoria hasta un máximo valor, y luego permanece constante en el tiempo, cuando se alcanza el estado estacionario, tal como se puede observar en la curva azul de la figura que se muestra a continuación. La curva verde representa el caso anterior sin amortiguamiento cuando λ = 0.

Registro gráfico del desplazamiento para ωf = ω , λ = 0 (curva verde) y λ > 0 (curva azul) .

Con la finalidad de ahondar un poco más en el análisis del sistema cuando entra en resonancia, se ofrece el applet que abajo se muestra donde se grafica la amplitud xo de las oscilaciones en función de la frecuencia. Dispone de los deslizadores Fo, M, k y λ para su control. La curva verde a trazos corresponde al movimiento forzado sin amortiguamiento (λ = 0), en cuyo caso ideal el sistema oscila hasta alcanzar una amplitud infinita; la roja, corresponde al modelo del movimiento oscilatorio amortiguado (λ > 0). Se puede apreciar el máximo de la amplitud xom como es de esperar; el mismo ocurre para el valor crítico de la frecuencia impulsora dado por ω = [ω_o² - 2 (λ/2M) ]^1/2.También se calculan los valores de xom , ω_o y ω. Se usaron unidades del Sistema Internacional de Unidades.

Disponible en: https://tube.geogebra.org/m/2353437

Actividades:

Para los valores indicados (M = 60 kg, k = 15 N/m, Fo = 2 N, λ = 7 kg/s), el sistema oscila en el estado transitorio y luego se estabiliza en el estado estacionario vibrando con la frecuencia ωc = 0,5 s^-1, como se puede comprobar en la figura que sigue.

Representación gráfica de la amplitud del desplazamiento xo en función de la frecuencia ωf.

4. Batidos o pulsaciones. La frecuencia impulsora es casi igual a la frecuencia del sistema (ω_f ≈ ω). En primer lugar se analiza el modelo más sencillo del sistema sin amortiguamiento (λ = 0), para los siguiente valores: λ = 0 kg/s , ωf = 5 s^-1, ω = 4,24 s^-1, Fo = 50 N. Por supuesto, el sistema oscila con la frecuencia promedio ωp = 0,5(ωf + ωo) y la amplitud de sus oscilaciones es modulada por la frecuencia ωm = 0,5(ωf - ωo); el período de las pulsaciones es Tp = Tm/2, donde Tm = 2 Tf T/(Tf - T) es el período de la modulación, Tf y T son los respectivos períodos de la fuerza impulsora y del sistema oscilante, respectivamente. Para los valores indicados arriba se tiene que ωf = 5 s^-1, ωm = 0,38 s^-1, Tm, = 16,5 s y Tp = 8,25 s; lo cual coincide con la lectura de la gráfica de la figura que se muestra.

Representación gráfica del desplazamiento para λ = 0 cuando ω_f ≈ ω.

La interpretación de estos valores es la siguiente. El sistema comienza a oscilar desde la posición de equilibrio hacia el punto de retorno positivo; a medida que oscila con la frecuencia promedio ωm = 4,62 s^-1la amplitud de las oscilaciones se incrementa hasta un máximo valor (aproximadamente a mitad del tiempo Tp), y luego decrece hasta un valor mínimo (ha transcurrido la otra mitad del tiempo Tp), para aumentar de nuevo, y continuar así indefinidamente. De esta manera, el desplazamiento es modulado en amplitud. Este comportamiento se repite en el tiempo (recordar que λ = 0). Tal cambio periódico temporal de la amplitud es lo que se conoce como pulsación o batido. Más adelante se retoma este concepto en el tema de ondas.

En segundo lugar se analiza el modelo con amortiguamiento (λ > 0) para los siguiente valores: λ = 4 kg/s , ωf = 5 s^-1, ω = 4,24 s^-1, Fo = 50 N. Se puede observar que, con la incorporación de la viscosidad, el sistema intenta oscilar en el estado transitorio con pulsaciones; sin embargo, en el estado estacionario se estabiliza, y continúa oscilando con la frecuencia impulsora ωf = 5 s^-1 y con el periodo Tf = 1,3 s como se indica en la figura adjunta.